Math Cornell Notes: Conquer Your Math Challenges
Struggling with math? Feeling overwhelmed by formulas and equations? This guide introduces the Cornell Notes method, a powerful tool transforming how you learn and master math concepts, from basic algebra to advanced calculus. By structuring your notes effectively, you'll improve comprehension, retention, and exam performance. Ready to become a math note-taking ninja?
Mastering the Three-Section Method: Your Note-Taking Powerhouse
The Cornell Notes method uses a three-section page layout:
Main Notes Section: This large area captures everything from class—lectures, examples, diagrams—serving as a comprehensive record of the lesson. Think of it as a detailed transcript of the learning experience.
Cue Column (Left-Hand Side): This smaller left-hand column is your personal study guide. As you take notes, jot down keywords, formulas, questions, or anything that requires further clarification or review. These act as prompts for self-testing and later review.
Summary Section (Bottom): After class, condense your main notes into a concise summary. This active recall process solidifies learning and pinpoints key takeaways. It’s your high-level overview of the entire lesson, perfect for rapid review before exams. Do you find summarizing challenging? Practice makes perfect!
This structured approach isn't merely about organization; it fosters active learning, transforming passive listening into active engagement with the material. Did you know that active recall significantly improves long-term retention?
Adapting Cornell Notes for Math: Making it Work for You
The true power of Cornell Notes lies in its adaptability. Here's how to optimize it for math:
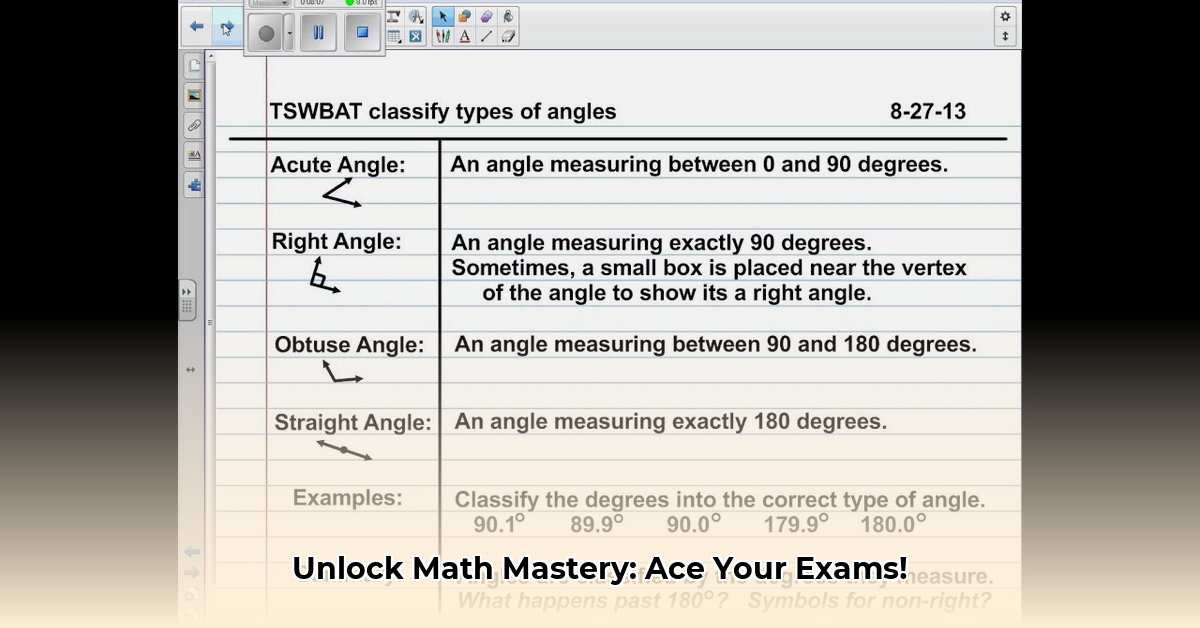
Definitions and Theorems – Concise and Clear: Write definitions and theorems accurately but briefly. Utilize mathematical symbols for efficiency and to better visualize relationships between concepts. Brevity is key to effective note-taking; strive for precision in every word.
Worked Examples – Understanding the Process: Don't just copy examples; dissect each step. Ask "why?" for every operation. If you encounter any confusion, flag it for clarification. Understanding why is more crucial than memorizing what.
Cue Column – Your Personal Math Formula Sheet: Use this section for formulas, key concepts, practice problems, and questions you generated. It becomes a tailor-made cheat sheet constantly updated with each learned concept.
Visual Aids – Draw It Out!: Math is inherently visual. Diagrams, graphs, and charts enhance understanding and recall. A visual representation often clarifies complex ideas more effectively than lengthy explanations.
Effective Summarization Techniques: The Secret to Retention
Summarization isn't about rewriting; it's about distillation. It's about extracting the core principles from your notes. Condense your detailed notes into a concise explanation of the lesson's core ideas, explaining the “how” and “why” behind the concepts you just learned.
Practice Examples: Seeing Cornell Notes in Action
Let's illustrate with diverse math problems:
| Problem Type | Notes Section | Cue Section | Summary |
|---|---|---|---|
| Solving Linear Equations | Steps: 1. Isolate x, 2. Simplify, 3. Check solution; Example: 3x + 7 = 13 | Linear Equation Steps, Inverse Operations | Successfully solved linear equations using inverse operations and verification. |
| Geometry (Area of a Triangle) | Formula: A = 0.5 * b * h; Example: Find area with base 6 cm, height 4 cm. | Area Formulas, Triangle Area Formula | Applied the triangle area formula (A = 0.5bh) to calculate area. |
| Calculus (Derivatives) | Power rule: d/dx (xⁿ) = nxⁿ⁻¹; Chain rule with examples. | Derivative Rules, Power Rule, Chain Rule | Mastered basic derivative rules, including applying the chain rule for complex functions. |
Review and Self-Testing: The Power of Active Recall
Regularly quiz yourself using your cue column. Turn those keywords and formulas into questions. This active recall strengthens memory and builds confidence. Consistent self-testing is far more effective than passive rereading.
Digital Tools: Embrace the Tech
Many digital tools facilitate Cornell note-taking. Explore options offering templates, cloud syncing, and searchable notes.
Addressing Common Challenges: Overcoming the Hurdles
Challenge: Feeling overwhelmed by complex concepts. Solution: Break down problems into smaller, manageable steps.
Challenge: Struggling with summarization. Solution: Practice summarizing simpler concepts first. Use your own words; avoid simply re-writing your notes.
Challenge: Inconsistent note-taking. Solution: Establish a consistent note-taking routine – treat it like any other important task.
Mastering Cornell Notes is a process, not a one-time fix. Consistent application will yield significant improvements in your math understanding and exam scores. Embrace this proven technique, and watch your math skills flourish!